- ...上田 哲史
![[*]](footnote.png)
- 徳島大学知能情報工学科
tetsushi@is.tokushima-u.ac.jp
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
川上 博
![[*]](footnote.png)
- 徳島大学電気電子工学科 kawakami@ee.tokushima-u.ac.jp
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... point)
![[*]](footnote.png)
- 固定点は不動点とも呼ばれている.つい
10年ぐらい前までは,不動点一点張りであったが,近年は固定点を使う頻度が増えて
きた.いずれもfixed point の訳である
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を省略する
![[*]](footnote.png)
- これからも誤解がでない範囲内で記号の省略をおこなう.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
線形行列微分方程式
![[*]](footnote.png)
- 係数行列
 は,状態変数
は,状態変数
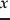 ,時間
,時間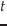 の
非線形関数となりうるので,線形というと面くらうかもしれない.しかし,
いま問題なのは
の
非線形関数となりうるので,線形というと面くらうかもしれない.しかし,
いま問題なのは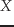 のダイナミックスであり,なんら状態変数に関与していない,という
意味で線形である.
のダイナミックスであり,なんら状態変数に関与していない,という
意味で線形である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の基本行列解
![[*]](footnote.png)
- この場合,レゾルベントという名前がついている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
の値によって平衡点の安定性を判別できたことを思いだそう
![[*]](footnote.png)
- 力学系がもともと
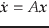 で表される線形系では,
直接
で表される線形系では,
直接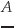 の固有値を調査することによって,解の大域的な挙動
まで分かってしまう
の固有値を調査することによって,解の大域的な挙動
まで分かってしまう
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
負の実部を持っていると,その平衡点が安定なのは一目瞭然であろう
![[*]](footnote.png)
- ここでの`安定'とは,あくまで平衡点の性質を言っているのであり,方程式
(26)の解の大域的な挙動を言っているのではない
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eqn:normal)をコンピュータで数値積分
![[*]](footnote.png)
- その
シミュレーション値が信用できるものかどうかは,チェックする
必要がある.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
をオンラインで変化させているとしよう
![[*]](footnote.png)
- 変化させたときのシステムの
初期値は,変化させる前の固定点の位置にしておくと観察しやすい.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
を得る
![[*]](footnote.png)
- これらはパラメータ
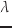 についての
微分であるため,解は基本行列解にはならず,ベクトル解となっている
ことに注意が必要である.式(51)をパラメータに関する変分方程式と
いう
についての
微分であるため,解は基本行列解にはならず,ベクトル解となっている
ことに注意が必要である.式(51)をパラメータに関する変分方程式と
いう
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
近似解の計算をゆだねる
![[*]](footnote.png)
- この点では式(45)は
正則であることが保証されている
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は固定した
![[*]](footnote.png)
- 表2 では に関する変分方程式しか求めていない
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
などの非常に有用な情報をもたらす
![[*]](footnote.png)
- これらの理由を考えてみよ
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)