式(2)をコンピュータで数値積分![[*]](footnote.png) させて,Poincaré写像によって,それが
写される固定点の様子を見てみる.周期外力を適当に設定して
1周期解を得ていることにしよう.
させて,Poincaré写像によって,それが
写される固定点の様子を見てみる.周期外力を適当に設定して
1周期解を得ていることにしよう.
いま,パラメータ
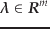 のうち,
のうち,
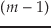 個の成分は固定し,残り1 つの
個の成分は固定し,残り1 つの
 をオンラインで変化させているとしよう
をオンラインで変化させているとしよう![[*]](footnote.png) .
すると,さまざまな点列の性質の変化が観測されるに
違いない.これらは固定点の分岐現象と呼ばれる.
固定点の分岐は,以下の3つの条件で起こる.
.
すると,さまざまな点列の性質の変化が観測されるに
違いない.これらは固定点の分岐現象と呼ばれる.
固定点の分岐は,以下の3つの条件で起こる.
- 接線分岐:固有値の1つが
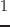 になる.
になる.
あるパラメータで突然,一つの固定点が別の位置にジャンプする.
(jump phenomenon).つまり軌道がそのパラメータで大きく形状を変える.
パラメータを逆方向に徐々に戻しても,ジャンプした
固定点は,すぐには元の位置に戻らないヒステリシス現象(histerisis phenomenon)
を示す.前節で説明した固定点追跡法では,この現象の近傍で式(14)
が非正則となるため,Newton 法がストップしてしまうであろう.
- 周期倍分岐:固有値の1つが
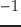 になる.
になる.
この分岐はあるパラメータで固定点が2点に分かれる(period doubling).
解軌道は,二重にだぶったように見える閉曲線として観察される.
これは新たに安定な固定点が2つ生まれ,変化前の安定な固定点は,
変化後に鞍型点となっている.
固定点が2つになったのではなく,3つになったことに注意.
- Neimark-Sacker分岐:2つの固有値が複素共役となり,単位円を横切る.
この分岐では,ある安定な固定点が突然不安定化し,その周りに準周期解
による不変閉曲線が現れる.
この分岐が現れない系もあらかじめ知ることができる(後述).
さて,これらの分岐曲線を得たいとしよう.上述のどの分岐においても,以下の
解析方法は同じである.
固定点の性質は,あらかじめ固有値として与えることができるので,
次の連立方程式を解けば分岐点の精密な位置が分かる.
![\begin{displaymath}
\begin{array}{l}
f_1(x_0,y_0,\lambda) - x_0 = 0 \\
f_2(x_0,...
...2\pi,x_0,y_0,\lambda) - \mu
\end{array}\right] = 0
\end{array}\end{displaymath}](img107.png) |
(7.41) |
この式(41)の第1,2式は固定点である条件,第3式は
指定された固有値に対して特性方程式の値がゼロになる条件,
言い替えると,ゼロでない固有ベクトルがある条件を表している.
 として,連立方程式を次の式でまとめる.
として,連立方程式を次の式でまとめる.
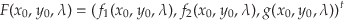 |
(7.42) |
ここで
 において,簡単に
行列式が展開できる:
において,簡単に
行列式が展開できる:
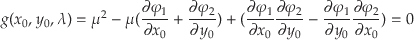 |
(7.43) |
分岐点のシューティングアルゴリズムとしては,前節と同様にNewton法を用いる.
式(13)を再掲する.
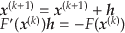 |
(7.44) |
ここで
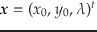 となっている.
この
となっている.
この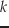 次近似におけるJocobi行列は,
次近似におけるJocobi行列は,
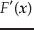 |
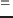 |
![$\displaystyle \left[
\begin{array}{lll}
\displaystyle
\frac{\partial f_1}{\part...
...ial \varphi_2}{\partial \lambda} \\
\displaystyle
a & b & c
\end{array}\right]$](img116.png) |
(7.45) |
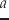 |
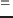 |
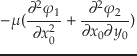 |
|
| |
|
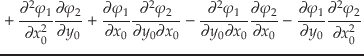 |
(7.46) |
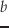 |
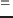 |
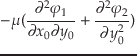 |
|
| |
|
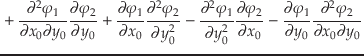 |
(7.47) |
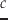 |
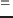 |
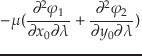 |
|
| |
|
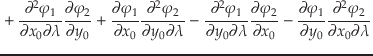 |
(7.48) |
となる.ここで
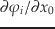 や
や
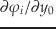 は,固定点追跡に
出てきた変分方程式の解を用いればよいと分かるだろう.すると
残りの
は,固定点追跡に
出てきた変分方程式の解を用いればよいと分かるだろう.すると
残りの
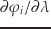 や,
2階偏微分のものはどうやって生成すればよいのだろうか.
や,
2階偏微分のものはどうやって生成すればよいのだろうか.
まず,パラメータによる微分
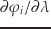 は,
式(16)について,パラメータを含めた解を,
は,
式(16)について,パラメータを含めた解を,
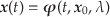 |
(7.49) |
とすると,この式のパラメータ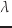 についての微分は,
についての微分は,
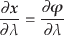 |
(7.50) |
となる.これを式(16)に代入することにより,線形な
微分方程式,
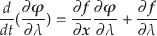 |
(7.51) |
を得る![[*]](footnote.png) .
これについて,前節のように
.
これについて,前節のように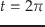 での値を数値的に解いてやればよい.
での値を数値的に解いてやればよい.
次に,二階の変数については,方程式(20)をさらに
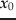 に
ついて微分したものを考えるとよい:
に
ついて微分したものを考えるとよい:
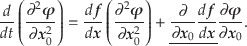 |
(7.52) |
もちろん,式中の
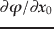 や
や
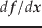 は式(21)を流用する.
下線部はテンソル積となって
複雑である.この式を第2変分方程式という.付録に第1,第2変分方程式に
ついてまとめた.
は式(21)を流用する.
下線部はテンソル積となって
複雑である.この式を第2変分方程式という.付録に第1,第2変分方程式に
ついてまとめた.
さて,この式(52)も同じく,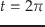 での値を数値的に求める
ことができると,
Jocobi行列の要素が全て決定できるので,分岐点の精密な
位置が算出できる.
での値を数値的に求める
ことができると,
Jocobi行列の要素が全て決定できるので,分岐点の精密な
位置が算出できる.
Subsections
User &
2017-09-07
![[*]](footnote.png) させて,Poincaré写像によって,それが
写される固定点の様子を見てみる.周期外力を適当に設定して
1周期解を得ていることにしよう.
させて,Poincaré写像によって,それが
写される固定点の様子を見てみる.周期外力を適当に設定して
1周期解を得ていることにしよう.
![]() のうち,
のうち,
![]() 個の成分は固定し,残り1 つの
個の成分は固定し,残り1 つの
![]() をオンラインで変化させているとしよう
をオンラインで変化させているとしよう![[*]](footnote.png) .
すると,さまざまな点列の性質の変化が観測されるに
違いない.これらは固定点の分岐現象と呼ばれる.
固定点の分岐は,以下の3つの条件で起こる.
.
すると,さまざまな点列の性質の変化が観測されるに
違いない.これらは固定点の分岐現象と呼ばれる.
固定点の分岐は,以下の3つの条件で起こる.
![]() として,連立方程式を次の式でまとめる.
として,連立方程式を次の式でまとめる.
![]() は,
式(16)について,パラメータを含めた解を,
は,
式(16)について,パラメータを含めた解を,
![[*]](footnote.png) .
これについて,前節のように
.
これについて,前節のように![]() に
ついて微分したものを考えるとよい:
に
ついて微分したものを考えるとよい:
![]() での値を数値的に求める
ことができると,
Jocobi行列の要素が全て決定できるので,分岐点の精密な
位置が算出できる.
での値を数値的に求める
ことができると,
Jocobi行列の要素が全て決定できるので,分岐点の精密な
位置が算出できる.