いま,パラメータは一定値に定めておく.したがって,以下の式では
変数 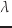 を省略する
を省略する
![[*]](footnote.png) .
固定点のだいたいの位置は,数値シュミレーションによって容易に得られる.
このデータから任意の精度の正確な位置がいま,知りたいとしよう.
それにはNewton法を用いる.
.
固定点のだいたいの位置は,数値シュミレーションによって容易に得られる.
このデータから任意の精度の正確な位置がいま,知りたいとしよう.
それにはNewton法を用いる.
Newton方のアルゴリズムを簡単に復習する.
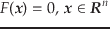 とすると,関数
とすると,関数
 の,
第
の,
第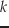 近似
近似
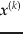 まわりのTaylor展開は,
まわりのTaylor展開は,
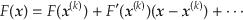 |
(5.10) |
で表される.ここで
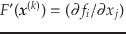 はJacobi行列である.近似値の修正量
はJacobi行列である.近似値の修正量
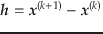 は次の式で与えられる.
は次の式で与えられる.
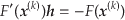 |
(5.11) |
Newton法は二次収束であり,かなりよい第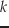 近似
近似
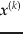 を与えたら,
数回の反復で精度の良い近似解が得られる仕組みになっている.
を与えたら,
数回の反復で精度の良い近似解が得られる仕組みになっている.
さて,Poincaré 写像の方程式(8)の固定点の近似値を
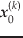 とする.いま,
とする.いま,
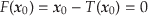 |
(5.12) |
としたとき,第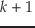 次の近似解を得るアルゴリズムは次のとおり.
次の近似解を得るアルゴリズムは次のとおり.
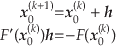 |
(5.13) |
ここで,
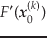 は初期値
は初期値
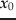 に関する微分による第
に関する微分による第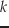 次の
Jacobi行列
次の
Jacobi行列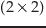 で,
で,
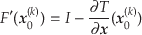 |
(5.14) |
![\begin{displaymath}
\frac{\partial T}{\partial \mbox{\boldmath$ x $}}(\mbox{\bol...
...\partial y_0} (2\pi, x_0^{(k)}, y_0^{(k)})
\end{array}\right]
\end{displaymath}](img43.png) |
(5.15) |
となる.ただし,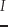 は
は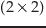 の単位行列である.
式(13)の第2式は,
の単位行列である.
式(13)の第2式は,
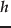 について,
Gaussの掃き出し法などで 解かなくてはならない.
について,
Gaussの掃き出し法などで 解かなくてはならない.
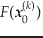 は関数値そのものを与えるとよいが,
問題は,式(15)の
Jacobi行列の要素(偏微分の値!)をどうやって求めるかである.
は関数値そのものを与えるとよいが,
問題は,式(15)の
Jacobi行列の要素(偏微分の値!)をどうやって求めるかである.
ちょっと元にもどって考えてみよう.
式(2)を書き直す:
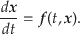 |
(5.16) |
ただし,
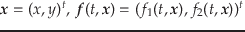 とする.
とする.
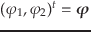 としたとき,
初期値
としたとき,
初期値
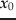 から出発する式(16)の解を
から出発する式(16)の解を
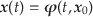 |
(5.17) |
としよう.
この解を式(16)に代入すると,
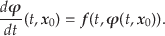 |
(5.18) |
この式を
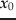 で微分する.すると,
で微分する.すると,
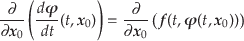 |
(5.19) |
左辺の微分の順序は変更できる.右辺も計算すると,
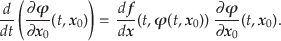 |
(5.20) |
この式は,わかりやすく書き換えると,
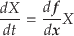 |
(5.21) |
となる.つまり
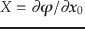 は
線形行列微分方程式
は
線形行列微分方程式![[*]](footnote.png) の基本行列解
の基本行列解 ![[*]](footnote.png) となっている.
この式(20)は式(16)の変分方程式といわれる.
となっている.
この式(20)は式(16)の変分方程式といわれる.
ところで
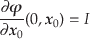 |
(5.22) |
である.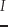 は
は の単位行列である.
式(22)を初期値として,式(20)を時刻
の単位行列である.
式(22)を初期値として,式(20)を時刻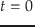 から
から
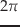 まで数値積分すれば,式(15)を求める
ことができ,Newton法によって精密な固定点の位置
まで数値積分すれば,式(15)を求める
ことができ,Newton法によって精密な固定点の位置
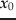 が
求められる.また
が
求められる.また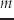 -周期点が求めたい場合は積分を
-周期点が求めたい場合は積分を まで
実行すればよい.
まで
実行すればよい.
User &
2017-09-07
![[*]](footnote.png) .
固定点のだいたいの位置は,数値シュミレーションによって容易に得られる.
このデータから任意の精度の正確な位置がいま,知りたいとしよう.
それにはNewton法を用いる.
.
固定点のだいたいの位置は,数値シュミレーションによって容易に得られる.
このデータから任意の精度の正確な位置がいま,知りたいとしよう.
それにはNewton法を用いる.
![]() とすると,関数
とすると,関数
![]() の,
第
の,
第![]() 近似
近似
![]() まわりのTaylor展開は,
まわりのTaylor展開は,
![]() とする.いま,
とする.いま,
![[*]](footnote.png) の基本行列解
の基本行列解 ![[*]](footnote.png) となっている.
この式(20)は式(16)の変分方程式といわれる.
となっている.
この式(20)は式(16)の変分方程式といわれる.