

Next: 4. Conclusions
Up: 3. Dynamical Properties of
Previous: 3.4 Dynamical Structure of
The familiar Lorenz equation is given by
 |
(18) |
Many research reports [Jackson, 1991; Argyris, 1994] mentioned its
bifurcation structure in the 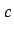 -
-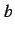 plane. We now show its
bifurcation sets in the
plane. We now show its
bifurcation sets in the 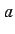 -
-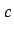 plane in comparison with Chen's
equation.
plane in comparison with Chen's
equation.
This system also has three equilibria: 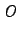 ,
, 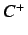 , and
, and 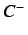 ,
and their topological properties are almost the same as that of
Chen's equation (7). Figure 16 shows
the bifurcation diagram of solutions of the Lorenz system
(18). There exist islands of period-locking, which
are the same as those shown in Fig. 2. The chaotic
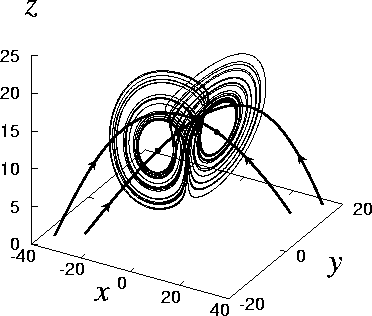
attractor, as shown in Fig. 17 (g), is widely
observed in this parameter plane.
,
and their topological properties are almost the same as that of
Chen's equation (7). Figure 16 shows
the bifurcation diagram of solutions of the Lorenz system
(18). There exist islands of period-locking, which
are the same as those shown in Fig. 2. The chaotic
attractor, as shown in Fig. 17 (g), is widely
observed in this parameter plane.
Figure 16:
Bifurcation diagram of the Lorenz system
(18). 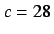 .
.
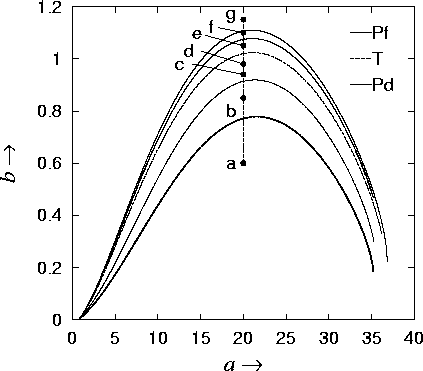 |
Figure 17:
Phase portrait of Eq. (18).
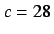 .
(a)
.
(a) 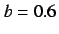 , (b)
, (b) 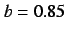 , (c)
, (c) 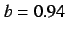 , (d)
, (d) 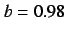 ,
(e)
,
(e) 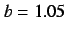 , (f)
, (f) 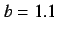 , (g)
, (g) 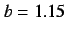 .
.
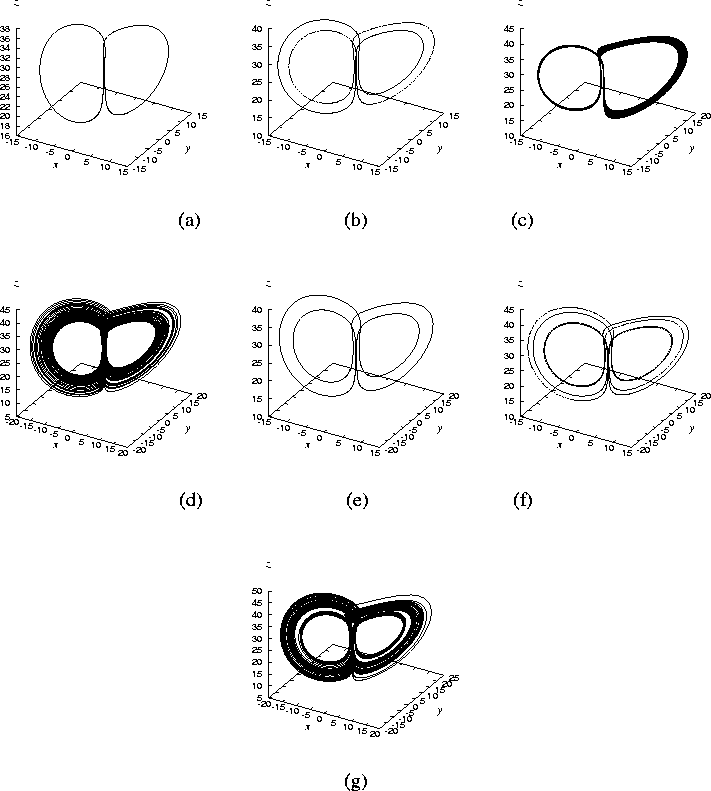 |
Hopf bifurcations at the equilibria, except for the origin, occurs
at the value of
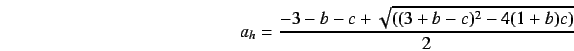 |
(19) |
When 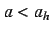 , the system orbit, starting from the neighborhood
of
, the system orbit, starting from the neighborhood
of 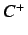 or
or 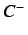 , is trapped into the chaotic attractor.
While if
, is trapped into the chaotic attractor.
While if 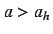 , the chaotic attractor is eventually absorbed
by
, the chaotic attractor is eventually absorbed
by 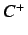 or
or 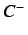 . It is the well-known ``crisis'' phenomenon.
. It is the well-known ``crisis'' phenomenon.
The stable manifolds of 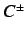 are very simple, as can be seen
from Fig. 18. The mechanism of chaos is
therefore completely different from Chen's strange attractor.
are very simple, as can be seen
from Fig. 18. The mechanism of chaos is
therefore completely different from Chen's strange attractor.
Figure 18:
Stable manifolds of 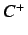 and
and 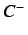 .
.
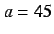 ,
, 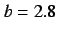 ,
, 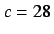 .
.
 |


Next: 4. Conclusions
Up: 3. Dynamical Properties of
Previous: 3.4 Dynamical Structure of
Tetsushi "Wahaha" UETA
�$BJ?@.�(B13�$BG/�(B1�$B7n�(B24�$BF|�(B

![]() ,
, ![]() , and
, and ![]() ,
and their topological properties are almost the same as that of
Chen's equation (7). Figure 16 shows
the bifurcation diagram of solutions of the Lorenz system
(18). There exist islands of period-locking, which
are the same as those shown in Fig. 2. The chaotic
attractor, as shown in Fig. 17 (g), is widely
observed in this parameter plane.
,
and their topological properties are almost the same as that of
Chen's equation (7). Figure 16 shows
the bifurcation diagram of solutions of the Lorenz system
(18). There exist islands of period-locking, which
are the same as those shown in Fig. 2. The chaotic
attractor, as shown in Fig. 17 (g), is widely
observed in this parameter plane.
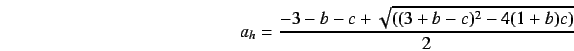
![]() are very simple, as can be seen
from Fig. 18. The mechanism of chaos is
therefore completely different from Chen's strange attractor.
are very simple, as can be seen
from Fig. 18. The mechanism of chaos is
therefore completely different from Chen's strange attractor.