2. Anti-Control of the Lorenz Equation

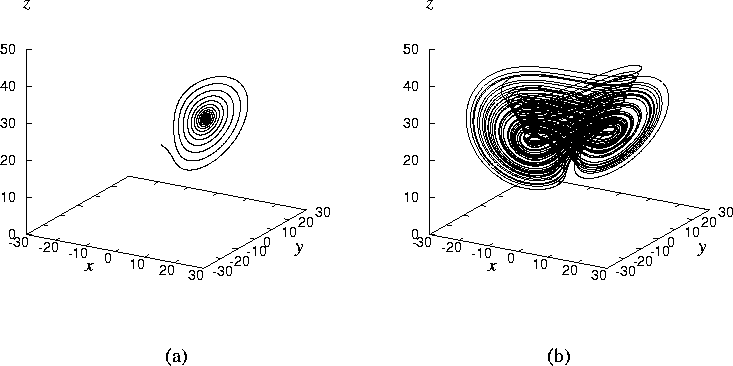
In this section, we focus on the creation of chaos with anti-control techniques. We try to destabilize some existing stable equilibria of non-chaotic system by using state feedback. This method not always yields chaotic situation, however; it may work out if the equilibria have hyperbolic structures in a globally bounded system.

Consider the controlled Lorenz equation:

$$\begin{array}{rcl} \displaystyle \frac{dx}{dt} & = & a (y - ... ...kip0.5ex} \displaystyle \frac{dz}{dt} & = & xy - bz \end{array}$$ (1)

where $a, b, c$ are constants, currently not in the range of chaos, and $u$ is a linear feedback controller of the form

$$u=k_1x+k_2y+k_3z\,,$$ (2)

in which $k_1, k_2, k_3$ are constant gains to be determined. The controlled system Jacobian, evaluated at $(x^*,y^*,z^*)$, is given by

$$J_{(x^*,y^*,z^*)} =\left[\begin{array}{ccc} -a & a & 0 \\ c+k_1-z^* & k_2 -1 & k_3-x^* \\ y^* & x^* & -b \end{array}\right]$$ (3)

To find the equilibria of the controlled Lorenz system (1)-(2), let

$$\begin{array}{rcl} \displaystyle a (y - x)=0\\ \noalign{\vs... ...\\ \noalign{\vskip0.5ex} \displaystyle xy - bz = 0 \end{array}$$ (4)

Obviously, $(0,0,0)$ is a trivial equilibrium.

To find non-zero equilibria, observe that the first equation of (4) yields immediately $x=y$, so that the third one gives $z=\frac{1}{b}\,x^2$. Therefore, the second equation of (4) leads to

$$x=y=\frac{1}{2}\,k_3\pm\frac{1}{2}\,\sqrt{k_3^2+4b(c+k_1+k_2-1)}$$ (5)

It can be easily seen from the Jacobian (3) that if this Jacobian is evaluated at the zero equilibrium, $(x^*,y^*,z^*)=(0,0,0)$, then $k_3$ does not contribute to its eigenvalues, which means $k_3$ does not contribute to the system Lyapunov exponents. Therefore, we may choose $k_3=0$ for simplicity. To further determine $k_1$ and $k_2$ for possible chaotic behavior of the system (1) under anti-control (2), we turn to the system Jacobian (3) evaluated at the two non-zero equilibria (5). To have chaotic behavior, these equilibria cannot be stable, or in other words, we have to have at least one unstable eigenvalue at each of these two equilibria. The Routh test reveals a simple possible choice, among several others, of

$$k_1=-\,a\qquad{\rm and}\qquad k_2=1+c$$

Luckily, computer simulations have shown that these gains indeed yield a successful anti-controller:

$$u = -\,a\,x +(1+c)\,y$$ (6)

which leads the controlled, currently non-chaotic Lorenz equation (1)-(2) to the following chaotic Chen's equation:

$$\begin{array}{rcl} \displaystyle \frac{dx}{dt} & = & a (y - ... ...kip0.5ex} \displaystyle \frac{dz}{dt} & = & xy - bz \end{array}$$ (7)

Figure 1(a) shows a phase portrait of the non-chaotic Lorenz equation with $a=35$, $b=8/3$, $c=28$, in which an orbit started from an arbitrary initial point is attracted into a sink. On the contrary, we see in Fig. 1 (b) a chaotic attractor in the anti-controlled system (7) with the same set of parameter values. Besides, as stated below, boundedness of the anti-controlled system is guaranteed. These results suggest that the anti-controlling action is effective to create chaotic behavior in some cases like this one.

Figure 1: Phase portraits. (a): Uncontrolled Lorenz system, (b): Anti-controlled Lorenz system. $a=35$, $b=8/3$, $c=28$. $(x_0, y_0, z_0) = (-3, 2, 20)$.