3.3 Bifurcations of Periodic Solutions

In this section, we fix $c=28$ and investigate the behavior of system limit cycles.

We use the Poincare mapping method to investigate the properties of periodic solutions of Eq. (7). We take an appropriate local plane as the Poincare section, for instance, $y=\sqrt {(2c-a)b}$ or $y = 0$, and then calculate the bifurcation parameter values by using the Poincare map and its derivatives.

There are three kinds of local bifurcations for periodic solutions in this system:

• tangent bifurcation: T
• pitchfork (symmetry-breaking) bifurcation: Pf
• period-doubling bifurcation: Pd

The parameter values that generate these bifurcations are calculated by simultaneously solving the fixed point of the Poincare map and the system characteristic equation.

Figure 2: Bifurcation diagram of Eq. (7). $c=28$.

Figure 3: Typical structure of the periodic-locking region.

Figure 4: Enlargement of Fig. 2.

Figure 2 shows a bifurcation diagram in the $a$-$b$ plane for periodic solutions. In this figure, roughly speaking, there exist three divisions in the plane. Each region has stable attractors, i.e., sinks ($C^{+}$ and $C^{-}$), chaos, and limit cycles. Many islands (windows) giving periodic solutions are embedded in the chaotic region. Each island is basically composed of a set of bifurcation curves (T, Pf, Pd), as illustrated by Fig. 3.

Figure 5: Phase portraits of stable attractors whose parameters are corresponding to Fig. 4 (a)-(k). (b), (c), (g) and (h) indicate two periodic solutions described by Eq. (17), simultaneously.

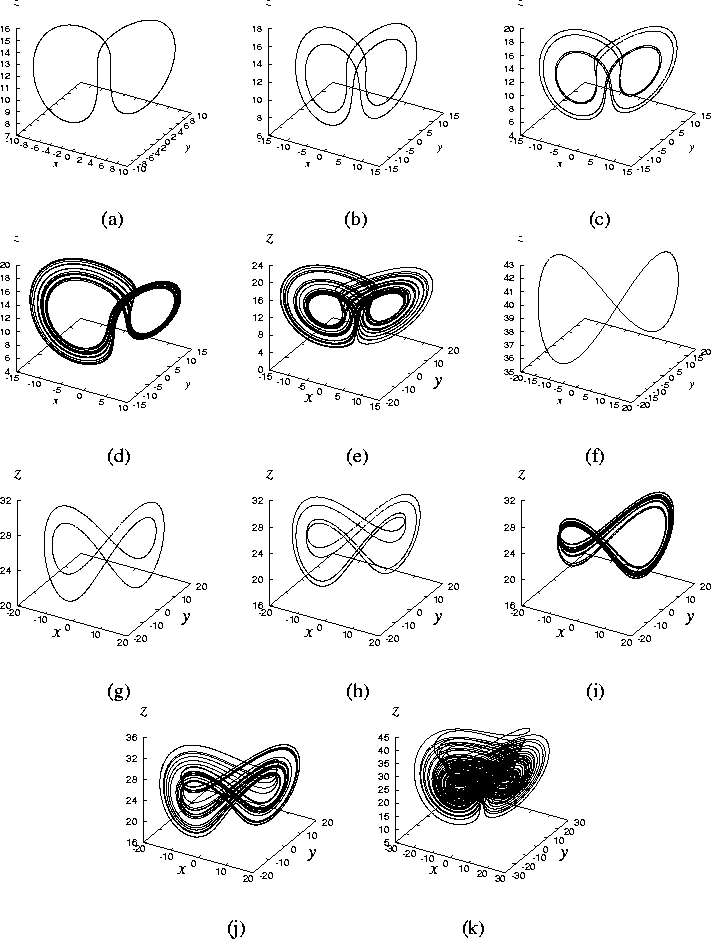Figure 4 shows an enlargement of Fig. 2. Let us first observe the responses of the system when the parameter $b$ changes gradually from the lower part to the upper part along the line $\overline{\mbox{ae}}$. The periodic solution, shown in Fig.5 (a), is generated by the tangent bifurcation T via intermittent chaos. This solution is divided into two stable limit cycles after crossing the pitchfork bifurcation Pf, see Fig 5 (b). They form the Lorenz-linkage [Jackson, 1991]. Let $\mbox{\boldmath$\ x $}(t) = \mbox{\boldmath$\ \varphi $}(t,\mbox{\boldmath$\ x $}_0)$ be a solution of this system with initial condition $\mbox{\boldmath$\ x $}_0 = \mbox{\boldmath$\ \varphi $} (0,\mbox{\boldmath$\ x $}_0)$. Let $\mbox{\boldmath$\ \varphi $}_1(t)$ and $\mbox{\boldmath$\ \varphi $}_2(t)$ be the limit cycles generated by Pf. The relationship between these two cycles is as follows:

$$\mbox{\boldmath$ \varphi $}_1(t,\mbox{\boldmath$ x $}_0) = P... ... = P \mbox{\boldmath$ \varphi $}_1(t,P\mbox{\boldmath$ x $}_0)$$ (17)

Each of them is bifurcated to period-2 solutions when crossing the period-doubling bifurcation $\mbox{Pd}_1$, see Fig. 5 (c). When these solutions meet $\mbox{Pd}_2$, we have period-4 solutions. Via period-doubling cascade, finally it develops into a chaotic attractor as shown in Fig. 5 (d). Thus, there exist two isolated chaotic attractors in the state space. It can be observed by further changing the value of $b$ that these isolated chaotic attractors are merged. The attractor looks like the Lorenz attractor, see Fig. 5 (e), namely, there are two spirals and the orbit tend asymptotically to some two-dimensional surface in the state space.

On the other hand, by changing parameter $a$ along the line $\overline{\mbox{fk}}$, Figs. 5 (f)-(k) are obtained, which show the corresponding phase portraits. We can see the same bifurcation scenario. However, the chaotic attractor shown in Fig. 5 (k) is somewhat different from a Lorenz-type attractor by means of its spiral shape over the two screws, which does not have the tendency to move to any two-dimensional surface. We further discuss this attractor in Sec.3.4.

Figure 6 shows bifurcation curves that form another island. Figures 7 (a)-(d) are phase portraits observed on the parameter sets a-d indicated in Fig. 6. Also, the same bifurcation scenario can be observed.

Figure 6: Enlargement of Fig. 4.

Figure 7: Phase portraits whose parameters are corresponding to Fig. 6 a-d.

Figure 10 is also an enlargement of the upper part of Fig. 2, showing regions sectioned by bifurcation curves. In each region, there exists at least one topologically different stable attractor against another region. The tangent bifurcation curve T for a limit cycle is coalesced by the pitchfork bifurcation curve Pf. Thus, two periodic orbit generated by Pf is immediately disappeared by T at the boundary of (A) and (F). In region (F), we have a chaotic attractor as shown in Fig. 8. This attractor is probably related to a kind of homoclinic orbits about $O$, since some parts of the orbit are tangent to the plane including unstable manifolds of $O$, as can be seen from Fig. 8 (a)-(d). This chaotic orbit changes its shape to be Lorenz-like, when the parameter is changed toward inside of region (F). This can be seen from Fig. 11. Further investigation of this orbit is very interesting but time-consuming, which will be summarized and presented in a future article. As the parameter set is changed from region (B) toward region (C), the limit cycle meets the period-doubling cascade diagram started from Pd. In region (C), there also exist chaotic solutions.

Figure: (a)-(c) A chaotic attractor observed near the boundaries of (A) and (F) in Fig. 10. (d): An enlargement around the origin. $a=41.0181$, $b=11.5$, $c=28$.

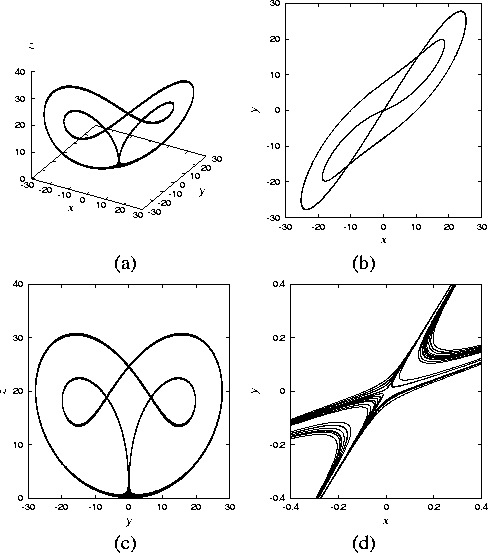The island composed of regions (D) and (E) showing periodic motions connects to region (B). Figures 9 show the corresponding Lyapunov exponents along $b=11$ from (A) to (F). From these exponents, it is seen that there exists a very narrow area exhibiting chaos between (C) and (D).

Figure 9: Lyapunov exponents. (a) $b=3$, (b) $b=11$, $c=28$.

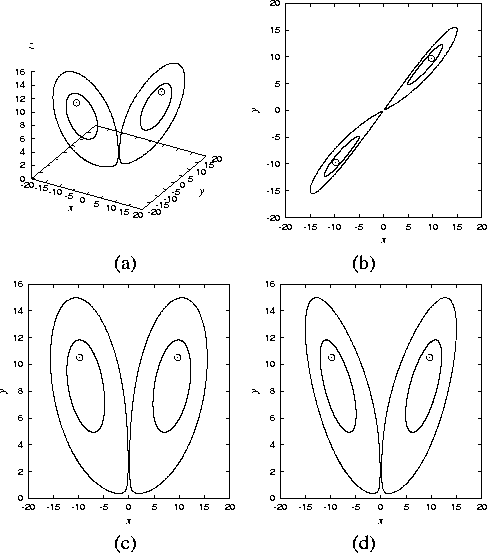
In Fig. 10, the curve H shows Hopf bifurcation for $C^{\pm}$ described by Eq. (16). There is no stable periodic solution in region (I), and there exist two stable limit cycles in region (G). In fact, there also exist two unstable (saddle-type) limit cycles in this region. Figure 12 shows these limit cycles and the unstable equilibria. These two cycles disappear when reaching the tangent bifurcation T. After this bifurcation, one can see a chaotic attractor as shown in Fig. 11. Note that this chaotic attractor can survive in regin (I); in other words, coexistence of stable equilibria and chaotic attractor occurs in region (I).

Figure 10: An enlargement of Fig. 2.

Figure 11: A typical chaotic attractor. $a=44$, $b=11$.

Figure 12: Attractors. dashed curve: unstable cycle; thin curve: stable cycle; small circle: unstable equilibrium. $a=47.4979$, $b=9$, $c=28$.