3.4 Dynamical Structure of the Chaotic Attractor

In this section, we focus our attention on the dynamical structure of the strange attractor shown in Figure 5 (k), where $(a,b,c)=(35,3,28)$. Figure 13 (a)-(c) show the projections of the attractor onto the $x$-$y$, $y$-$z$, and $x$-$z$ planes, respectively. The origin $O$ is a one-dimensionally unstable saddle and its eigenvalues are $-30.836$, $23.836$ and $-3.0$. $C^{\pm} = (\pm 3\sqrt{7}, \pm 3\sqrt{7}, 21)$ are two-dimensionally unstable and their corresponding eigenvalues are $-18.428$ and $4.214\pm i 14.885$.

Figure 13: Various projections on the phase planes for the chaotic attractor shown in Fig. 5 (k). (a): $x$-$y$, (b): $x$-$z$, (c): $y$-$z$. (d): A perspective view (the view point is on $x=y$).

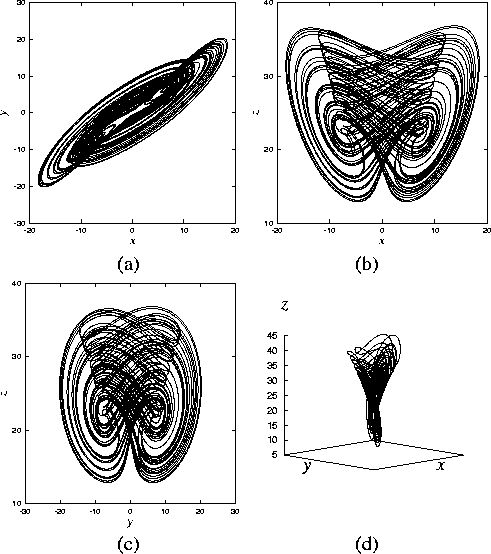
Figures 14(a)-(c) show Poincare mapping on several sections. Several sheets of the attractors are visualized. In Fig. 14(d), it is clear that some sheets are folded.

Figure 14: Poincare map. (a): $y = 0$; (b) $y=\sqrt {(2c-a)b}$; (c): $z=2c-a$, $y > x$; (d): an enlargement of (c).

Figure 15 shows the shapes of the stable manifolds for $C^{\pm}$. These one-dimensional manifolds wander over the chaotic attractor. Note that stability of these stable manifolds (negative eigenvalue) around $C^{\pm}$ is very strong.

Figure 15: Stable manifolds of $C^{+}$ and $C^{-}$. $a=35$, $b=3$, $c=28$. The chaotic attractor is superimposed in (c) and (d).

Let us summarize how the attractor is formed. The orbit starting from an initial point whose values are sufficiently big must move to the $z > 0$ portion of equilibria because the instability of the unstable manifold of $O$ is very strong and grows up toward $z > 0$. Then the orbit draws elliptically in the $x$-$y$ plane, decreasing the value $z$. It flows along the stable manifold of $C^{\pm}$, and takes a shape like a spiral in the $y$-$z$ or $x$-$z$ plane. After this, the orbit reached near $C^{\pm}$ goes away rapidly and scarcely turns on the 2-dimensionally unstable manifold of $C^{\pm}$ since the real part of the unstable eigenvalue is comparatively big. The orbit is then trapped into the unstable chaos as shown in Fig. 5 (i) for awhile. Finally, the orbit is lifted up along the unstable manifold of $O$. We can see that the stable manifolds of $C^{\pm}$ plays an important role in the generation of the strange attractor.