

Next: 3.3 Bifurcations of Periodic
Up: 3. Dynamical Properties of
Previous: 3.1 Some Mathematical Properties
The dynamical system described by Eq. (7) has three
equilibria if 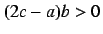 :
:
By considering a Jacobian matrix for one of these equilibria and
calculating their eigenvalues, we can investigate the stability
of each equilibrium based on the roots of the system characteristic
equation.
Here, we first observe some bifurcations of the equilibria existing
in Eq. (7). We gradually change the values of 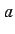 .
When
.
When 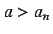 , the origin
, the origin 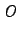 is the only equilibrium and it is
a sink, where
is the only equilibrium and it is
a sink, where
 |
(14) |
is the parameter value at which the sink changes to a node. Then,
a pitchfork bifurcation for 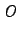 emerges at the value of
emerges at the value of
 |
(15) |
At this moment, 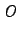 changes to a one-dimensionally unstable saddle
and, at the same time, two symmetric sinks are generated, so we
have three equilibria when
changes to a one-dimensionally unstable saddle
and, at the same time, two symmetric sinks are generated, so we
have three equilibria when 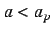 . The parameter
. The parameter 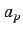 is also
the tangent/saddle-node bifurcation value for both
is also
the tangent/saddle-node bifurcation value for both 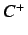 and
and
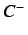 . Note that these bifurcations do not depend on parameter
. Note that these bifurcations do not depend on parameter
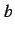 .
.
Hopf bifurcations emerges from these sinks, at the value of
 |
(16) |
where the complex conjugate eigenvalues are
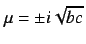 .
When
.
When
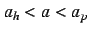 ,
, 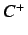 and
and 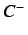 are
both stable sinks. At
are
both stable sinks. At 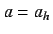 , however, they change to two
two-dimensional unstable saddles, and two isolated limit cycles
are generated around them, respectively. These simulation results
are combined into the figures shown in the next section.
, however, they change to two
two-dimensional unstable saddles, and two isolated limit cycles
are generated around them, respectively. These simulation results
are combined into the figures shown in the next section.


Next: 3.3 Bifurcations of Periodic
Up: 3. Dynamical Properties of
Previous: 3.1 Some Mathematical Properties
Tetsushi "Wahaha" UETA
�$BJ?@.�(B13�$BG/�(B1�$B7n�(B24�$BF|�(B
![]() :
:
![]() .
When
.
When ![]() , the origin
, the origin ![]() is the only equilibrium and it is
a sink, where
is the only equilibrium and it is
a sink, where
