

Next: 3.2 Bifurcations of Equilibria
Up: 3. Dynamical Properties of
Previous: 3. Dynamical Properties of
This section discusses some basic dynamical properties of Chen's
equation (7).
This system has the same complexity as the Lorenz equation
-- they are both
three-dimensional autonomous with only two quadratic terms.
However, it is topologically not equivalent to the Lorenz equation.
This can be rigorously proved by showing that a homeomorphism of
the form
![\begin{displaymath}
\left\{\begin{array}{l}
x_C = \xi(x_L,y_L,z_L)\\ [3pt]
y_C =...
...L,y_L,z_L)\\ [3pt]
z_C = \zeta(x_L,y_L,z_L)
\end{array}\right.
\end{displaymath}](img50.gif) |
(8) |
does not exist, where 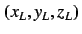 and
and 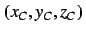 are
the variables of the Lorenz and Chen equations, respectively.
The proof can be carried out by taking a time derivative on
(8) and then performing some straightforward but
tedious algebra, which leads to a system of algebraic equations
without solutions.
are
the variables of the Lorenz and Chen equations, respectively.
The proof can be carried out by taking a time derivative on
(8) and then performing some straightforward but
tedious algebra, which leads to a system of algebraic equations
without solutions.
It is easy to see that this equation has a trivial property
of symmetry: the equation is invariant under the following
transformation:
 |
(9) |
Then, let us rewrite Eq. (7) in the following vector
form:
 |
(10) |
where
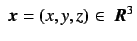 , and
, and
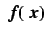 is the right-hand side of Eq. (7). The transformation
(9) can now be denoted as
is the right-hand side of Eq. (7). The transformation
(9) can now be denoted as
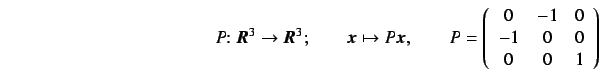 |
(11) |
which satisfies
 |
(12) |
The dynamics of the system is affected by this symmetry. For
example, in the projection of its orbits onto the phase plane,
variable 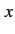 and
and 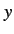 are symmetric with respect to the origin.
Besides, this hints that pitchfork bifurcation for equilibria
and periodic solutions are possible.
are symmetric with respect to the origin.
Besides, this hints that pitchfork bifurcation for equilibria
and periodic solutions are possible.
Let us examine the stability of Chen's system. It is easy to
verify that the system is globally, uniformly and asymptotically
stable about its zero equilibrium if 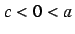 . This can be checked
by using the Lyapunov function
. This can be checked
by using the Lyapunov function
which gives
Next, let us consider a volume in a certain domain 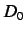 of the
state space. Notice that
of the
state space. Notice that
 |
(13) |
We always use a set of parameters satisfying 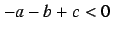 , such
as
, such
as
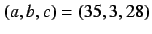 [Chen & Ueta, 1999]. This means that the
dynamical system (7) is guaranteed to be dissipative,
so the volume of any attractor of the system must be zero. The
orbit flows into a certain bounded region as
[Chen & Ueta, 1999]. This means that the
dynamical system (7) is guaranteed to be dissipative,
so the volume of any attractor of the system must be zero. The
orbit flows into a certain bounded region as
 .
.


Next: 3.2 Bifurcations of Equilibria
Up: 3. Dynamical Properties of
Previous: 3. Dynamical Properties of
Tetsushi "Wahaha" UETA
�$BJ?@.�(B13�$BG/�(B1�$B7n�(B24�$BF|�(B
![\begin{displaymath}
\left\{\begin{array}{l}
x_C = \xi(x_L,y_L,z_L)\\ [3pt]
y_C =...
...L,y_L,z_L)\\ [3pt]
z_C = \zeta(x_L,y_L,z_L)
\end{array}\right.
\end{displaymath}](img50.gif)
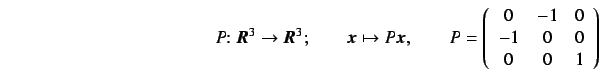
![]() . This can be checked
by using the Lyapunov function
. This can be checked
by using the Lyapunov function