
Next: 4.3 Forced BVP oscillator
Up: 4 Examples
Previous: 4.1 A Discrete Chaotic
We also confirm the availability of our method to continuous-time
system. The following differential equation is a mathematical model
of the neural oscillator:
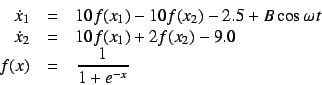 |
(10) |
The system has a limit cycle in the autonomous system; i.e., 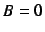 .
By changing
.
By changing 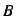 or
or 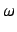 , generation of quasi-periodic solution,
chaotic motion, and frequency entrainment are observed.
Then we construct the Poincaré mapping
, generation of quasi-periodic solution,
chaotic motion, and frequency entrainment are observed.
Then we construct the Poincaré mapping 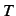 to the periodic
solution, calculate isoclines and bifurcation curves in
to the periodic
solution, calculate isoclines and bifurcation curves in 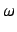 -
-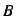 plane. Figure 4 shows a bifurcation diagram of this
system. It is clear that same structures are found with
Fig. 1.
plane. Figure 4 shows a bifurcation diagram of this
system. It is clear that same structures are found with
Fig. 1.
図 4:
Bifurcation diagram of Eq. (10).
|
|
図 5:
Phase portrait: Poincaré mapping on the NS bifurcation
with
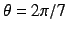 .
.
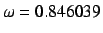 ,
, 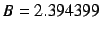 ,
,
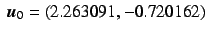 .
.
|
|


Next: 4.3 Forced BVP oscillator
Up: 4 Examples
Previous: 4.1 A Discrete Chaotic
tetsushi
平成15年6月16日