

Next: 3 Calculation of NS
Up: Calculation of the Isocline
Previous: 1 Introduction
Let 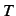 be a map described as follows:
be a map described as follows:
 |
(1) |
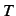 has explicit parameters
has explicit parameters
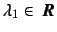 and
and
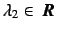 and
and 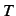 is a
is a 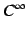 map for these parameters.
Then the fixed point
map for these parameters.
Then the fixed point
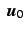 of Eq.(1) is given as
of Eq.(1) is given as
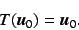 |
(2) |
Assume now that this fixed point has at least a pair of complex conjugate
multipliers described by:
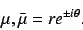 |
(3) |
where, 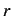 is the radius,
is the radius, 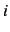 is the imaginary unit and
is the imaginary unit and 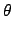 is the argument.
If
is the argument.
If 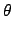 is specified,
the location and the parameter value of the fixed point
forms an isocline as the another parameter value changes.
is specified,
the location and the parameter value of the fixed point
forms an isocline as the another parameter value changes.
Let
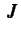 be the Jacobian matrix of
be the Jacobian matrix of 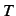 around
around
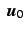 and
and 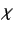 be the corresponding characteristic equation:
be the corresponding characteristic equation:
![\begin{displaymath}
\chi = \mathop{\rm det}\nolimits [\mbox{\boldmath$ J $}- r e^{i\theta}] = \Re \chi + i \Im \chi = 0
\end{displaymath}](img28.png) |
(4) |
where 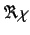 and
and 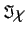 show the real and imaginary part
of the characteristic equation.
show the real and imaginary part
of the characteristic equation.
To calculate the location of the fixed point with specified
argument, the following simultaneous equation should be
solved with
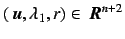 by using Newton's method:
by using Newton's method:
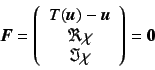 |
(5) |
Then the Jacobian matrix of the Eq.(5) is written as follows.
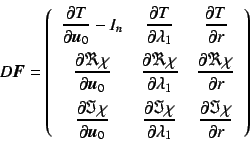 |
(6) |
Note that all factors of the matrix in Eq.(6)
are obtained by solving the variational equation of 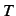 .
If
.
If 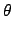 is fixed as an appropriate value within
is fixed as an appropriate value within ![$[0, \pi]$](img34.png) ,
the isocline is drawn in the parameter plane
,
the isocline is drawn in the parameter plane 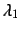 -
-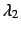 by plotting the solution
by plotting the solution 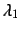 as the incremental parameter changes.
as the incremental parameter changes.
Now suppose that the parameter region in which the fixed point exists is
already obtained.
Firstly specifying 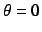 or
or 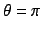 , we obtain an isocline
which splits the parameter region into two parts; the part has is a sink,
the other has a stable node.
Therefore this isocline can be regarded as a bifurcation curve.
For any rational ratio with
, we obtain an isocline
which splits the parameter region into two parts; the part has is a sink,
the other has a stable node.
Therefore this isocline can be regarded as a bifurcation curve.
For any rational ratio with 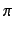 of
of 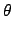 ,
the corresponding isocline shows
instantaneous phase around the fixed point and it is
deeply related to the NS bifurcation and existence of
frequency entrainment regions.
Along this isocline, the stability is indexed by
,
the corresponding isocline shows
instantaneous phase around the fixed point and it is
deeply related to the NS bifurcation and existence of
frequency entrainment regions.
Along this isocline, the stability is indexed by 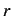 , i.e.,
within
, i.e.,
within 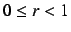 , we have a stable sink, and
, we have a stable sink, and
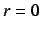 shows a super stable sink.
shows a super stable sink.


Next: 3 Calculation of NS
Up: Calculation of the Isocline
Previous: 1 Introduction
tetsushi
平成15年6月16日
![]() be the Jacobian matrix of
be the Jacobian matrix of ![]() around
around
![]() and
and ![]() be the corresponding characteristic equation:
be the corresponding characteristic equation:
![]() by using Newton's method:
by using Newton's method:
![]() or
or ![]() , we obtain an isocline
which splits the parameter region into two parts; the part has is a sink,
the other has a stable node.
Therefore this isocline can be regarded as a bifurcation curve.
For any rational ratio with
, we obtain an isocline
which splits the parameter region into two parts; the part has is a sink,
the other has a stable node.
Therefore this isocline can be regarded as a bifurcation curve.
For any rational ratio with ![]() of
of ![]() ,
the corresponding isocline shows
instantaneous phase around the fixed point and it is
deeply related to the NS bifurcation and existence of
frequency entrainment regions.
Along this isocline, the stability is indexed by
,
the corresponding isocline shows
instantaneous phase around the fixed point and it is
deeply related to the NS bifurcation and existence of
frequency entrainment regions.
Along this isocline, the stability is indexed by ![]() , i.e.,
within
, i.e.,
within ![]() , we have a stable sink, and
, we have a stable sink, and
![]() shows a super stable sink.
shows a super stable sink.