


Next: About this document ...
拡張BVP発振器における振動停止現象について
On Suppression of Oscillation in the Modified BVP Oscillator
| 上田 哲史 |
川上 博 |
| T. Ueta |
H. Kawakami |
| (徳島大学) |
Figure 1:
拡張BVP発振器
![\includegraphics[scale=0.75]{BVPextend.eps}](img11.png) |
拡張BVP発振器は,弛張発振をともなう
3階自律系のカオス力学系である[1].
図1 に回路図を示す.
網がけされている部分が2次元 BVP発振器であり,拡張した
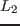 ,
, 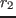 のダイナミクスが,どう発振器全体に影響するかは
興味深い問題である.
のダイナミクスが,どう発振器全体に影響するかは
興味深い問題である.
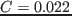 [
[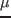 F],
F],
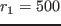 [
[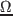 ],
],
 [mH] に選び,
[mH] に選び,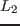 ,
, 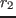 を解放除去した
2次元 BVP発振器は自励発振する.
その原因は原点の Hopf 分岐であることが明らかになっている[2].
を解放除去した
2次元 BVP発振器は自励発振する.
その原因は原点の Hopf 分岐であることが明らかになっている[2].
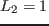 [mH],
[mH], 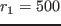 [
[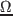 ] として,
弛張振動を示す状態に設定した.そこで,
] として,
弛張振動を示す状態に設定した.そこで,
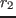 を大きい値から徐々に減少させて振動の変化を観察した.
を大きい値から徐々に減少させて振動の変化を観察した.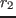 が大きいうちは
が大きいうちは 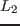 に流入する電流は小さく,2次元BVP発振そのもので
あるが(図2(a)),
突如
に流入する電流は小さく,2次元BVP発振そのもので
あるが(図2(a)),
突如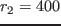 [
[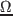 ] 付近で振動が停止する(図2(b)).このとき,
他に安定な平衡点やリミットサイクルはない.
その後,さらなる
] 付近で振動が停止する(図2(b)).このとき,
他に安定な平衡点やリミットサイクルはない.
その後,さらなる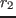 の減少によって再び発振が生じる(図2(c)(d)).
以下ではこれらの現象を数理的に解析する.
の減少によって再び発振が生じる(図2(c)(d)).
以下ではこれらの現象を数理的に解析する.
Figure 2:
実測値.
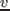 と
と 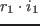 を測定した.
(a)
を測定した.
(a) 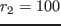 [k
[k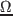 ].
]. 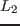 ,
, 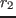 解放除去と同効果.約6[kHz].
(b)
解放除去と同効果.約6[kHz].
(b) 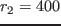 [
[ ]程度,振動停止.
(c)
]程度,振動停止.
(c) 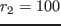 [
[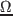 ]程度.振動復活,約 34[kHz].
(d)
]程度.振動復活,約 34[kHz].
(d) 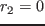 [
[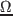 ](
](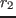 の短絡除去).振幅が非常に大きい.
の短絡除去).振幅が非常に大きい.
|
|
Figure 3:
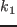 -
-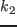 平面における分岐図.
平面における分岐図.
|
|
まず,回路方程式に対し正規化を施すと次の3階自律系を得る:
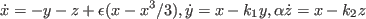 |
(1) |
ここで,3次特性で近似した非線形コンダクタンスは,測定から
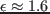 と同定された.
と同定された.
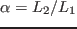 であり,上記の回路パラメータでは
であり,上記の回路パラメータでは  となる.
式(1)の数値計算においても,上記と同様な現象が確認された.
そこで,原点について
となる.
式(1)の数値計算においても,上記と同様な現象が確認された.
そこで,原点について 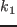 -
-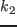 平面でのHopf分岐集合を求めた.
図3を参照.
正の抵抗値
平面でのHopf分岐集合を求めた.
図3を参照.
正の抵抗値  ,
, 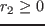 は,
は,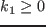 ,
,  に対応している.
に対応している.
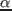 ,
, 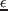 を固定すれば,分岐集合は
を固定すれば,分岐集合は 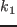 ,
, 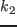 の関数となり,
の関数となり,
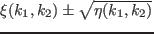 の形を取る.図中ではこの符号に合わせて
の形を取る.図中ではこの符号に合わせて
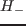 ,
, 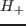 とした.上記の発振停止はこれら二つの Hopf 分岐が関与していた.
とした.上記の発振停止はこれら二つの Hopf 分岐が関与していた.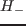 は
は
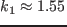 を漸近線として持つ双曲線であり,
他方の曲線は
を漸近線として持つ双曲線であり,
他方の曲線は 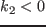 の領域で現れる.
の領域で現れる.
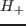 は,
は,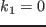 を変曲点とするわずかな歪みを持つが,
ほぼ至るところ直線となる.
を変曲点とするわずかな歪みを持つが,
ほぼ至るところ直線となる.
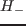 より上部は低い周波数の発振領域,
より上部は低い周波数の発振領域,
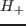 より下部は高い周波数の発振領域となる.
Hopf分岐後のリミットサイクルの角周波数を,図3 中に
数値(単位は[deg/sec]) として記入している.両分岐集合の持つ
周波数の差が大きいことが分かる.
次にこの分岐図の
より下部は高い周波数の発振領域となる.
Hopf分岐後のリミットサイクルの角周波数を,図3 中に
数値(単位は[deg/sec]) として記入している.両分岐集合の持つ
周波数の差が大きいことが分かる.
次にこの分岐図の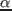 ,
, 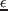 依存性を調査した.
依存性を調査した.
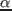 を変化させても分岐図にはほどんど影響がなく,
また,
を変化させても分岐図にはほどんど影響がなく,
また,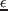 を
を
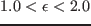 の実用範囲で
変化させても,双曲線の漸近線が若干移動するものの,
位相的には同じ分岐図となることが分かった.
つまり,図1 の回路構成では,
分岐図は定性的に図3の形状になり,
回路パラメータに非依存であると言ってよい.
原点のみに関する supercritical Hopf 分岐で,一つのパラメータ値変更に
よって二種類の異なる周波数の発振が得られる力学系は例がないと考えられる.
この研究は,日本学術振興会科研費若手(B)15760293 の補助を受けている.
の実用範囲で
変化させても,双曲線の漸近線が若干移動するものの,
位相的には同じ分岐図となることが分かった.
つまり,図1 の回路構成では,
分岐図は定性的に図3の形状になり,
回路パラメータに非依存であると言ってよい.
原点のみに関する supercritical Hopf 分岐で,一つのパラメータ値変更に
よって二種類の異なる周波数の発振が得られる力学系は例がないと考えられる.
この研究は,日本学術振興会科研費若手(B)15760293 の補助を受けている.
文献:
[1]吉永哲哉,慶応義塾大学博士論文,1992.
[2]北島博之,徳島大学博士論文, 1998.



Next: About this document ...
User &
2015-08-04
![\includegraphics[scale=0.75]{BVPextend.eps}](img11.png)
![]() ,
, ![]() のダイナミクスが,どう発振器全体に影響するかは
興味深い問題である.
のダイナミクスが,どう発振器全体に影響するかは
興味深い問題である.
![]() [
[![]() F],
F],
![]() [
[![]() ],
],
![]() [mH] に選び,
[mH] に選び,![]() ,
, ![]() を解放除去した
2次元 BVP発振器は自励発振する.
その原因は原点の Hopf 分岐であることが明らかになっている[2].
を解放除去した
2次元 BVP発振器は自励発振する.
その原因は原点の Hopf 分岐であることが明らかになっている[2].
![]() [mH],
[mH], ![]() [
[![]() ] として,
弛張振動を示す状態に設定した.そこで,
] として,
弛張振動を示す状態に設定した.そこで,
![]() を大きい値から徐々に減少させて振動の変化を観察した.
を大きい値から徐々に減少させて振動の変化を観察した.![]() が大きいうちは
が大きいうちは ![]() に流入する電流は小さく,2次元BVP発振そのもので
あるが(図2(a)),
突如
に流入する電流は小さく,2次元BVP発振そのもので
あるが(図2(a)),
突如![]() [
[![]() ] 付近で振動が停止する(図2(b)).このとき,
他に安定な平衡点やリミットサイクルはない.
その後,さらなる
] 付近で振動が停止する(図2(b)).このとき,
他に安定な平衡点やリミットサイクルはない.
その後,さらなる![]() の減少によって再び発振が生じる(図2(c)(d)).
以下ではこれらの現象を数理的に解析する.
の減少によって再び発振が生じる(図2(c)(d)).
以下ではこれらの現象を数理的に解析する.